Printers Network Graph
I. Beginnings
For my project, I chose to look at the connections between publishers in the eighteenth century. The reason was simple: I was caught early on by the fact that so many of the same names showed up in the publication info fields of each book. That is, you might see “James Dodsley” across as many as twenty different works, and he usually worked with the same cadre of individuals. This lead me to suspect that these publishers - and indeed it should be no shock - were friends, comrades, spent time together, etc. Or perhaps they were not social with each other in that way, but they each were part of an elaborate web of working relationships. I wanted to see who worked with who, and how large these webs were: how many people they each encompassed. As it turns out, when you include all the data we’ve got, some of these webs of connected publishers are very, very, very large. So large as to be almost impossible to analyze. But I will try.
I also chose this project because I wanted a recourse to a skill I had already developed, but hadn’t used for some time: coding, specifically in Python and C++. I had taken C++ a year ago at Swarthmore, and began with the semi-ludicrous idea that I could code this all in C++ and put in online in C++ (I didn’t even know that you need to use JavaScript to put things online). I was quickly brought to reason, and I brushed up on the Python I’d learned some three years ago. I created a Python program which generated a graph, in which nodes represent the names of printers and edges represent that they worked together. I have inserted the graph here:
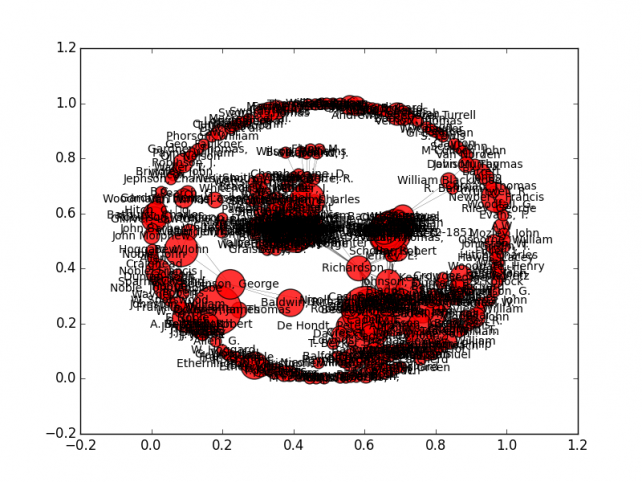
Yes, it’s overwhelming. Not that my final result got that much less overwhelming. But the Python program had a few problems. First, as I had failed to understand, you can’t just “put” a Python program online. You can take its output and reformat it in JavaScript, which I eventually did. Secondly, the graph generated by my program was basically unusable, because it dealt with so much data. It did, however, have a large advantage over my ultimate product: the nodes and edges in it were weighted. This was easy to do in Python, as I understand Python, and hard to do in JavaScript, as I’m still really knew to JS. It was hard enough to simply make the graph in JS. So, looking at this early attempt, you can see that the weight of a node indicates that a publisher published more or less books, with large nodes indicating more (obviously). The weight of an edge (or link between two publishers) corresponds to the number of books that those two publishers published together. This is of course really useful information, since in my final product, all one can tell is that two publishers knew each other. In fact, it emerges in this early graph that some publishers who had relatively small working networks, such as the brothers Robert and James Dodsley (the latter of whom I already mentioned), published quite a lot of books. The Dodsleys almost exclusively published as a duo, and thus had a small network, but their nodes are still quite large. Thus, it could be an expansion of my final result to introduce correspondent node size and edge weight to the JavaScript file.
With the help of Nabil Kashyap of Swarthmore, the Digital Humanities Librarian there, I made a new Python program which creates a JSON object, which is then read into a JavaScript program which uses the d3 library to generate a graph.
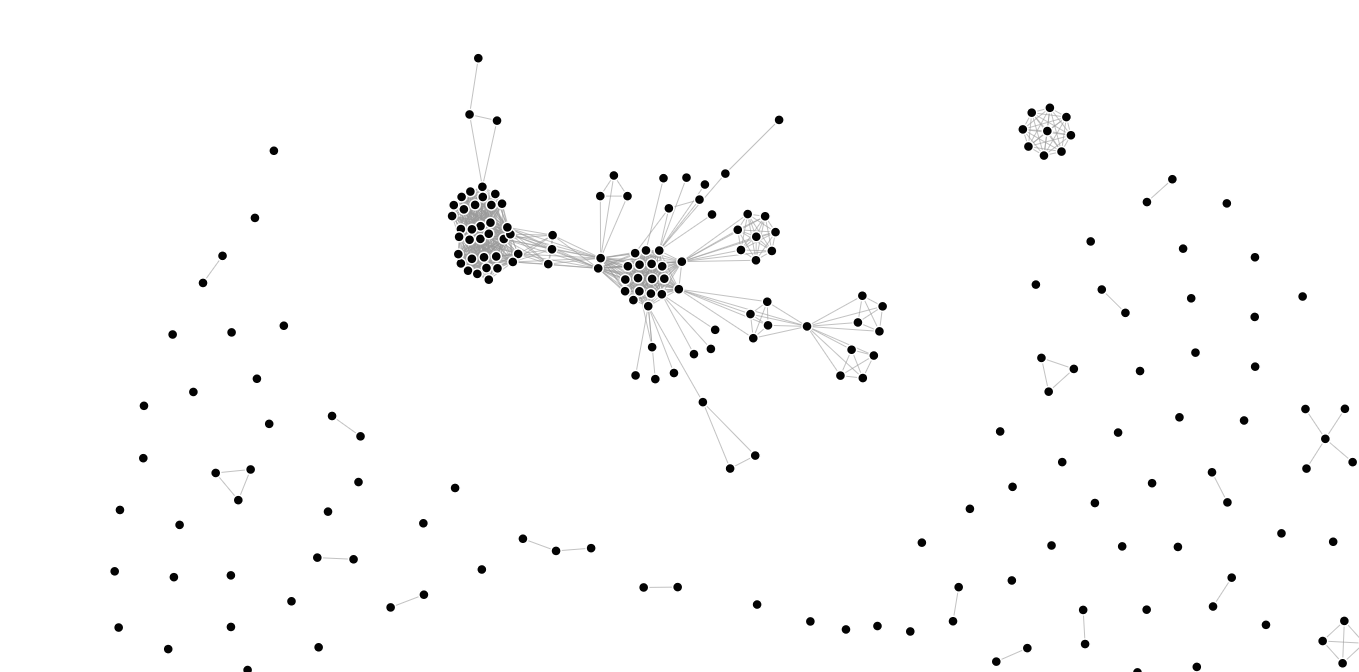
A preview of the resulting graph is below. You can also click through to the full, interactive version. You will have to scroll around to see the graph in its entirety. You can also mouse over a node to see which name it corresponds to. The code for the graph is hosted here.
Graph 1
II. Analysis
In this section, I will discuss findings. A few things are visible immediately from even a cursory glance at the graph: two main clusters emerge, surrounded by a large scattering of mostly unconnected nodes. These clusters represent the unconnected worlds of London and Dublin printing, which is my first finding: there is, in our data, literally no overlap between London and Dublin printing in the eighteenth century. No one in these two camps worked together. The Dublin cluster is the smaller of the two, and is more compact. The London cluster is actually made up of two clusters, linked through several publishers: J. Harris, E. Jeffrey, and R. Scholey worked with J. Johnson and J. Richardson, who in turn worked with the second cluster in this larger London cluster. That cluster is made up of such publishers as P. A. De Hondt and Thomas Lowndes. The first cluster of this larger London cluster (which will hereafter be referred to a Cluster A, with its sub-clusters A1 and A2, respectively), linked to R. Scholey, J. Harris, and E. Jeffrey, contains names like Thomas Payne and Andrew Strahan. (This cluster is A1, whereas the De Hondt-Lowndes cluster is A2.) One immediate question that emerges relates to the separation of these two groups: why are they only connected through these tenuous links? Why are they not all in one massive cluster, as in the Dublin cluster (Cluster B)? With a little bit of searching on VIAF, we can find out that:
- J. Johnson is Joseph Johnson (1738-1809).
- J. Richardson is Jonathan Richardson the Elder (1665-1745) or Younger (1694-1771).
- R. Scholey doesn’t show up in VIAF.
- J. Harris is either James Harris (1709-1780), John Harris (1667?-1719), or John Harris (active 168-1739 or 1740).
- E. Jeffrey is absent from VIAF.
Thus we only get one definite hit by checking VIAF. Before I proceed, I want to bring attention to a methodological problem with the process I used to generate this graph: because all data was pulled from the 700 fields, the same publisher may be represented by different nodes due to different spellings. So if Joseph Johnson was J. Johnson in one record, and Joseph Johnson in another (due to the oversight of a past cataloger, for instance), he would get two nodes. I had hoped this irregularity would come out in the wash, since we’re dealing with so much data - but it’s hard to say for sure if it did.
Another place to look for the identity of R. Scholey and E. Jeffrey would be in a book of printers, although this data is not necessarily authorized. (Of course, the above graph includes unauthorized data as well - which is something I may remedy, later on.)
If we assume that Richardson and Harris were contemporaries of Johnson (as indeed, they worked with him), then we can more easily choose their identities: J. Richardson must be The Younger, because Joseph Johnson was hardly alive when the Elder Richardson was active. Same goes for Harris: the only Harris contemporaneous with J. Johnson was James Harris.
Thus having placed three out of these five printers, the larger question still remains: why are they the crux that links these two gigantic groups of London publishers? On hypothesis is time: we’re looking at two generations of publishers, connected by a few people who spanned both generations. Indeed J. Harris, J. Johnson, and J. Richardson all lived an exceptionally long time — around 70 years each.
To test this hypothesis, I’ll now check out the VIAF entries of several publishers in each subcluster:
- A1: William Lowndes lived from 1652-1724. James Asperne, however, lived from 1757-1820.
- A2: Thomas Caslon died in 1783. R. Baldwin lived from 1737-1810. W. Johnston died in 1804. William Strahan lived between 1715-85.
I thought that, as a test, I would generate a new graph which takes only the names of authorized publishers. This should help eliminate much of the problem mentioned above, as well as resulting in data that is easier to locate and deal with.
Graph 2

In this version, cluster A is much smaller. It has lost the entirety of cluster A1, becoming in effect just A2. A1, meanwhile, is floating off the the side, making a third cluster (though a small one), which I will call cluster C. Thus the massive amalgam of London printers is actually not so massive, if one excludes unauthorized data. Thus it is only the Dublin printers (Cluster B) who emerge as a tightly-packed, integrated network after this filtering process. This does not mean, however, that London printers were not similarly connected, as unauthorized data may still be truthful.
I decided to go one step further, and eliminate outlying records: that is, records that included far more printers than any others. This was on the suspicion that these records could be single-handedly responsible for the large clusters we see: that is, if the printers in these records only worked on one book but all worked on it, they would emerge as a dominant, indeed monolithic cluster. To cut them out, I eliminated all clusters of more than 20 names — of which there are four. (Do these correspond to Clusters A and B?) This, however, does not affect the result at all.
I also went as far as to cut out all publishers who didn’t work with anyone else. This reduces clutter in the graph.
Graph 3

Finally, I wanted to try to address the problem I pointed out above, about duplicate nodes for the same printer. I had already noticed that “Richard Baldwin” appeared as both “Baldwin, R.” and “Baldwin, Richard” in two subclusters that should be connected, but are not.
Graph 4

This was my attempt at a “clean data” version of the prior graph (#3). It didn’t work perfectly: I still cannot figure out why “De Hondt, P” is appearing on the graph, for instance, when his name should have been corrected to “De Hondt, Peter Abraham” — and, in fact, the name “De Hondt, P” does not appear in the list of nodes I’m using to generate this graph. Which utterly mystifies me. It may be a problem with the way bl.ocks, the website I’m using to generate these graphs, accesses information from Gist, a part of github used to host small files. Perhaps bl.ocks is pulling data from the wrong JSON files — for instance, from the file I used to make Graph 3. Then Graph 4 would be exactly the same as Graph 3. But they are not the same, and I can’t figure out what else could be wrong.
There remain, however, some useful takeaways from Graph 4, imperfect as it might be. Here, the London subclusters A1 and A2 are again linked into a large cluster A, but only tenuously, via the persons of “Cadell, T” and “Payne, Thomas”. (Whereas before, the linking was much stronger.) So who were Cadell, T (who really should be Cadell, Thomas, according to the revisions I made when cleaning the text), and “Payne, Thomas”? These two Thomases were a bridge between two large networks of printers not otherwise connected.
Yet my analysis remains limited. It will be very important in the future to add node and edge weights, since right now we still cannot really answer the question of, Well, were these networks really that large? Certainly the contained a large number of individuals, but maybe those people only collaborated once, on one book, all together. Which would make them not all that vital.
Thomas Cadell, it turns out, lived from 1742-1802 and seems to have worked with publishers like “W. Strahan” and “T. Becket” (according to VIAF). Indeed, in my graph he is connected to William Strahan and Thomas Becket. It seems he worked in “The Strand”. Thomas Payne (1719-1799) published at least one book with a large network of other publishers, including, according to VIAF, “J. F. and C. Rivington, and J. Wilkie; T. Payne, and Son; S. Crowder, and R. Baldwin; T. Lowndes; T. Caslon and B. Law.” This could account for the cluster to which he, through Cadell, forms a vital link.
Thus even with all my work and this technology, it seems hard to conceptualize, from our twenty-first century standpoint, the real interconnectedness of 18th century printers. To do so, my project would need to expand in several ways.
III. Expansion
Clearly it is now necessary that, for this graph to give us real usable information about the prominence of certain printers in the 18th century and of the networks they worked in, it become weighted, so that we can easily see who really produced how much stuff. As of now, it remains shadowy; we know people were connected (and others not) but we don’t know the strength of these bonds. I want to find out whether or not this relatively young industry, that of printing, and especially novel-printing (still not a well respected enterprise, I’d guess) enforced strong ties, perhaps of necessity, between its practitioners. One way to know, aside from reading the history, is to visualize the closeness of those ties. But seeing them isn’t fully enough to know what they mean, except relative to each other. For example, a powerful bond between two printers may represent that they printed more books together than they did with other printers, but it doesn’t mean that they were actually friends. It doesn’t mean that they were part of a new, rebellious movement aiming to bring the novel to the masses. That, I’m not sure how to test.
However, it may document to some extent the social lives of printers in the 18th century, provided we assume - as may be reasonable, I’m not fully sure - that work acquaintances probably account for at least part of a person’s social circle.
What has emerged definitively from this work are the clusters I mention above. That not a single printer from the Ireland cluster (B), at least in our data, worked with a single printer from the London clusters (A1 and A2), is almost shocking. How is it that there was no working partnerships between these people, when the Dubliners were constantly filching the Londoners’ books? Perhaps the rivalry — and patriotism — of the two groups was too great to allow for such fraternizing. Or economic reasons simply did not make it practicable.
Finally, this data is not quite up to date. The file used to generate it includes all data generated by END between 2013 and 2015, up to July 27th. However, at the time of this post, we have data up till August 7th, with many more finalized records. Someone with more digital know-how, and more time, than I, could go and collate those individual “finalized record” files into one master XML file, as before, which could be used to generate even more complete data. And who knows, maybe the Dublin and London crowds really did work together after all.
Before I end, I want to go back to the “good” of this project. There are some real, though perhaps smaller, takeaways generated here. For instance, in the London Subcluster A2 (De Hondt-Lowndes), “Lowndes, Thomas,” emerges as a pivotal figure, who worked with 4 publishers who worked with no one else from that subcluster: in fact, only two of them (Collins, B, and Knox, John) worked with anyone else at all, and that was with each other. “Dilly, E”, also in A2, serves as an important link, like Payne and Cadell, to another subcluster, perhaps again because of only one work. A third cluster, C, also exists in this graph, containing printers like Stanley Crowder — who formed a pivotal link between the three triangular subgroups of this cluster. Crowder was active in London at the same time as many of the publishers from A, so it’s surprising cluster C is unconnected from it — and yet maybe we are simply lacking the data for that.
The density of the Dublin cluster B is also awe-inspiring. These publishers clearly worked very closely together. Almost everyone worked with everyone, especially as you zoom-in more towards the tightly-packed center of the cluster. It’s nearly impossible to tell who was pivotal here, as everyone worked with everyone, but better graphing software — or perhaps just better code, as d3 really is quite flexible — could make that clearer. Again, I think this project could live on in many incarnations.
I, for one, had a lot of fun with it.
IV. Resources
I have put all the code I used online at https://gist.github.com/ianhoffman. There is a python file, “xml-parse.py” that I used to parse the XML file containing all our finalized records from over the years. It is currently modified to omit any publishers that are unauthorized or that didn’t work with anyone else (thus, it is set-up to generate graph 4). It is also self-correcting, but imperfectly (as graph 4 is imperfect). If you keep working on it, you can get in touch with me, ianhoffman10@gmail.com, for some guidance.
This python program was used to generate JSON files, which are then used by javascript to make d3 graphs. That’s all here too, under 4 files: “cleanData.html” makes Graph 4, “Authorized.json” makes Graph 2, “allFiles.json” makes Graph 1, and “index.html” makes Graph 3.
Special thanks to Nabil Kashyap for all his help.
